D Y Patil International University, Akurdi, Pune

EME 1006    Engineering Mathematics

Teaching Scheme	Credits	Examination Scheme
TH: 03Hrs/Week	04	TH: 100 Marks
TUT: 01Hrs/WeekBatchwise		TW:25 Marks
Total Hrs:35		Total Marks:125

 

Prerequisite:  Matrices and Determinants, Differentiation and Integration, Differential Equation,

Course Objectives:

1)      To develop mathematical and computational skills

2)      To enhance analytical and logical thinking power of students and deploy these skills effectively in their disciplines.

3)      To equip the students with concepts and techniques in Matrices and Differential Calculus.

4)      To enable the students to apply concepts and techniques in Ordinary & Partial differentiation.

 

Course Outcomes:After successful completion of the course, students will be able to:

CO1: Solve system of linear equations by using the concept of Rank of the matrix

CO2:  Find Eigen Values and Eigen Vectors of the matrix

CO3:Solve and apply the knowledge of ordinary differential equation of first order and first degree

CO4:  Deal with derivative of functions of several variables

CO5:  Apply partial differentiation to calculate Errors, Approximations and Extreme values

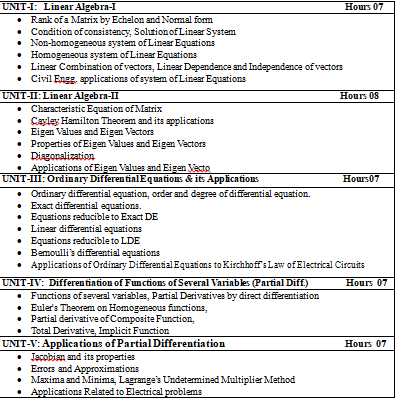
Unit I: Linear Algebra-I:        (7 Hrs.)

Unit II: Linear Algebra-II:     (7 Hrs.)

Unit III: Ordinary Differential Equations & its Applications:         (7 Hrs.)

Unit IV: Differentiation of Functions of Several Variables (Partial Diff.): (7 Hrs.)

Unit V: Applications of Partial Differentiation:                                   (7 Hrs.)

Engineering Mathematics-I

Teaching Scheme	Credits	Examination Scheme
TH: 03 Hrs/Week	04	TH: 100 Marks
TUT: 01 Hrs/Week		TW: 25 Marks
Total Hrs: 36		Total Marks:125

Course Objectives:

1)      To develop mathematical and computational skills

2)      To enhance analytical and logical thinking power of students and deploy these skills effectively in their disciplines.

3)      To equip the students with concepts and techniques in Matrices and Differential Calculus.

4)      To enable the students to apply concepts and techniques in Ordinary & Partial differentiation.

 

Course Outcomes: After successful completion of the course, students will be able to:

CO1: Solve system of linear equations by using the concept of Rank of the matrix

CO2:  Find Eigen Values and Eigen Vectors of the matrix

CO3:  Solve and apply the knowledge of ordinary differential equation of first order and first degree

CO4:  Deal with derivative of functions of several variables

CO5:  Apply partial differentiation to calculate Errors, Approximations and Extreme values

Prerequisite:  Matrices and Determinants, Differentiation and Integration, Differential Equation,    

Prerequisite:

Matrices and Determinants, Differential & Integral calculus, Differential equations of first order & first degree, Vector Algebra

Course Objectives:

1)      To develop mathematical and computational skills

2)      To enhance analytical and logical thinking power of students and deploy these skills effectively in their disciplines.

3)      To enable the students with skills in differential equations and numerical techniques

 

Course Outcome:

On Completion of course learner will be able to:

1.      Solve higher order Linear differential equations

2.      Apply LDE to solve Civil Engineering Problems

3.      Apply the numerical techniques to solve system of linear equations

4.      Use the numerical methods to solve ordinary differential equations

5.      Perform Vector differentiation and analyse the vector fields

Course Content:

Unit 1: Higher order Linear Differential Equations    (7 Hrs.)       

·         LDE of nth order with constant coefficients,

·         Complementary Function,

·         Particular Integral  

·         General Solution of LDE by General Method

·         General Solution of LDE by Short-Cut Methods

·         General Solution of LDE by Variation Parameter Method

 

Unit 2: Applications of Linear Differential Equations    (7 Hrs.)

·         Simultaneous Differential Equation

·         Symmetric simultaneous Differential Equation

·         Applications of LDE Modeling of problems on bending of beams, whirling of shafts and  mass-spring systems

·         Applications of LDE-Modeling of Electrical circuits

 

Unit 3: Numerical Solutions of System of Linear Equations       (7 Hrs.)

·         Gauss-Elimination method.

·         Gauss -Jordan method.

·         Gauss -Seidel method.

·         Jacobi’s iterative method

·         LU Decomposition Method

 

Unit 4: Numerical solutions of ordinary differential equations:          (7 Hrs.)                      

·         Picard’s method

·         Euler’s method

·         Modified Euler’s method

·         4th order Runge- Kutta method

·         Predictor-Corrector methods

 

Unit 5: Vector Differential Calculus      (8 Hrs.)                                         

·         Vector differentiation,

·         Vector differential operator,

·         Gradient, Divergence and Curl,

·         Directional derivative,

·         Solenoidal, Irrotational and Conservative fields,

·         Scalar potential, Vector Identities