D Y Patil International University, Akurdi, Pune
Search results: 1884
- Teacher: Dr Rishikant Rajdeepak
- Teacher: Varsha Sambhaje
- Teacher: Suprabhat Sinha
- Teacher: Dr Vandna Srivastava
|
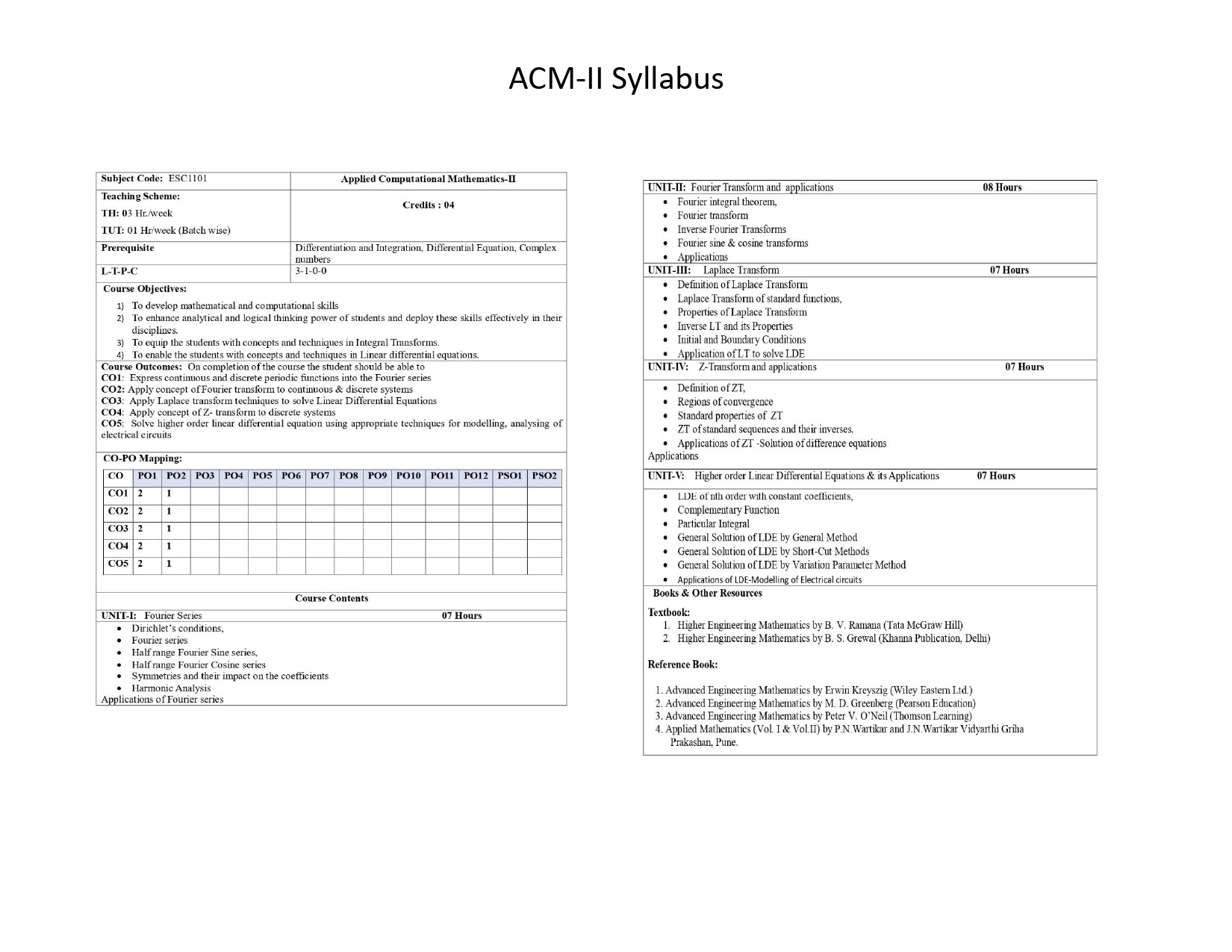
Subject Code: ESC1101 |
Applied Computational Mathematics-II |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Teaching Scheme: TH: 03 Hr./week TUT: 01 Hr/week (Batch wise) |
Credits : 04
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Prerequisite |
Differentiation and Integration, Differential Equation, Complex numbers |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
L-T-P-C |
3-1-0-0 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Course Objectives: 1) To develop mathematical and computational skills 2) To enhance analytical and logical thinking power of students and deploy these skills effectively in their disciplines. 3) To equip the students with concepts and techniques in Integral Transforms. 4) To enable the students with concepts and techniques in Linear differential equations. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Course Outcomes: On completion of the course the student should be able to CO1: Express continuous and discrete periodic functions into the Fourier series CO2: Apply concept of Fourier transform to continuous & discrete systems CO3: Apply Laplace transform techniques to solve Linear Differential Equations CO4: Apply concept of Z- transform to discrete systems CO5: Solve higher order linear differential equation using appropriate techniques for modelling, analysing of electrical circuits
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
CO-PO Mapping:
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Course Contents |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
UNIT-I: Fourier Series 07 Hours |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
· Dirichlet’s conditions, · Fourier series · Half range Fourier Sine series, · Half range Fourier Cosine series · Symmetries and their impact on the coefficients · Harmonic Analysis Applications of Fourier series |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
UNIT-II: Fourier Transform and applications 08 Hours |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
· Fourier integral theorem, · Fourier transform · Inverse Fourier Transforms · Fourier sine & cosine transforms · Applications |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
UNIT-III: Laplace Transform 07 Hours |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
· Definition of Laplace Transform · Laplace Transform of standard functions, · Properties of Laplace Transform · Inverse LT and its Properties · Initial and Boundary Conditions · Application of LT to solve LDE |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
UNIT-IV: Z-Transform and applications 07 Hours |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
· Definition of ZT, · Regions of convergence · Standard properties of ZT · ZT of standard sequences and their inverses. · Applications of ZT -Solution of difference equations Applications |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
UNIT-V: Higher order Linear Differential Equations & its Applications 07 Hours |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
· LDE of nth order with constant coefficients, · Complementary Function · Particular Integral · General Solution of LDE by General Method · General Solution of LDE by Short-Cut Methods · General Solution of LDE by Variation Parameter Method · Applications of LDE-Modelling of Electrical circuits |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Books & Other Resources Textbook: 1. Higher Engineering Mathematics by B. V. Ramana (Tata McGraw Hill) 2. Higher Engineering Mathematics by B. S. Grewal (Khanna Publication, Delhi)
Reference Book:
1. Advanced Engineering Mathematics by Erwin Kreyszig (Wiley Eastern Ltd.) 2. Advanced Engineering Mathematics by M. D. Greenberg (Pearson Education) 3. Advanced Engineering Mathematics by Peter V. O’Neil (Thomson Learning) 4. Applied Mathematics (Vol. I & Vol.II) by P.N.Wartikar and J.N.Wartikar Vidyarthi Griha Prakashan, Pune. Theory & Tutorial/Practical Class
Tutorial: i) Tutorial for the subject shall be engaged in minimum three batches (batch size of 22 students maximum) per division. ii) Term work shall consist of five assignments on each Unit-I to Unit-V and is based on performance and continuous internal assessment. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
- Teacher: Dr. Vanita Daddi
- Teacher: Sudhir Nanaso Narale

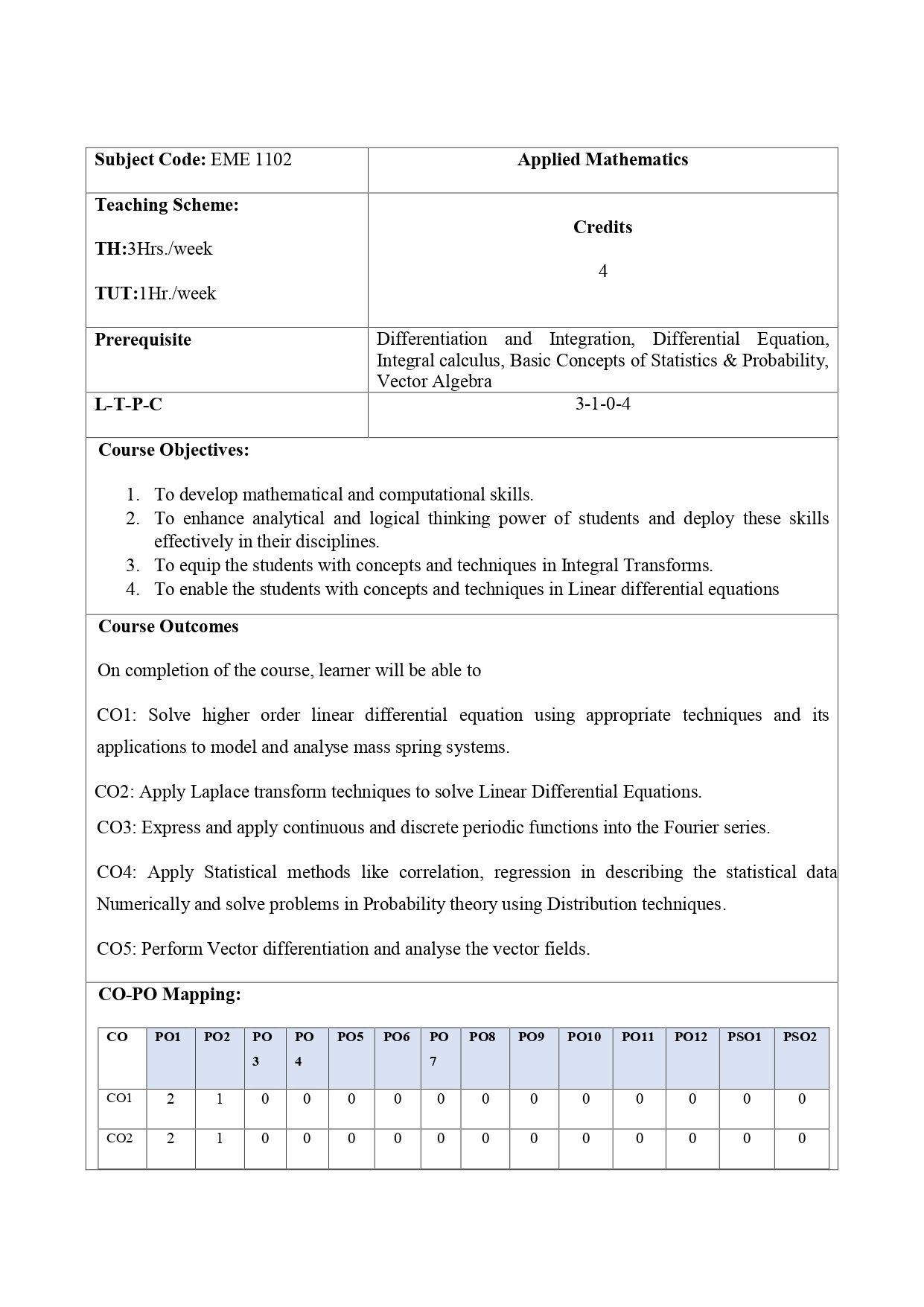
Unit I: Higher order Linear Differential Equations: (7 Hrs.)
LDE of nth order with constant coefficients,
Complementary Function
Particular Integral
General Solution of LDE by General Method
General Solution of LDE by Short-Cut Methods
General Solution of LDE by Variation Parameter Method
Mathematical Modeling of Chemical Engg. Problem
Unit II: Laplace Transform: (7Hrs.)
Definition of Laplace Transform
Laplace Transform of standard functions,
Properties of Laplace Transform
Inverse LT and its Properties
Application of LT to solve LDE
Unit III: Fourier Series: (7 Hrs.)
Dirichlet’s conditions,
Fourier series
Half range Fourier Sine series
Half range Fourier Cosine series
Harmonic Analysis
Applications of Fourier series – Harmonic Analysis, Modelling of Vibrating String
Unit IV: Fourier Transform: (7 Hrs.)
Fourier integral theorem,
Fourier transform,
Inverse Fourier Transforms
Fourier sine & cosine transforms
Applications of Fourier transforms
Unit V: Vector Differential Calculus: (7 Hrs.)
Vector differentiation,
Vector differential operator,
Gradient, Divergence and Curl,
Directional derivative,
Solenoidal, Irrotational and Conservative fields,
Scalar potential, Vector Identities
- Teacher: Mr Umesh Narkhede
- Teacher: Mrs.Mayura Abhijit khanore
- Teacher: Ms Yashswee Ghorpade
- Teacher: Dr. Lubna Shaik
- Teacher: Ms Naasrin Israiel Shaikh
- Teacher: Ms Varshini Dayanand Kore
- Teacher: Dr. Ragini Pandey
- Teacher: Dr. Sanjay Kumar
- Teacher: Ms. Surbhi Pandya
- Teacher: Varshini Dayanand Kore
- Teacher: Dr. Sanjay Kumar
- Teacher: Dr Sangeeta Benni
- Teacher: Dr. Vandana Patil
- Teacher: Mr. Vivek Prakash Magar
- Teacher: Dr. Dipika Pradhan
- Teacher: Dr. Rahul Sharma
- Teacher: Dr. Dipika Pradhan
- Teacher: Dr. Rahul Sharma
- Teacher: Dr. Prateek Srivastav
- Teacher: Ms Unnati Sunil Darak
- Teacher: Dr. Satyen Marathe
- Teacher: Mr. Ajinkya Hiran
- Teacher: Mr. Ajinkya Hiran
- Teacher: Dr. Somya Dubey
- Teacher: Mr. Ajinkya Hiran
