Sem II (2024-2025)

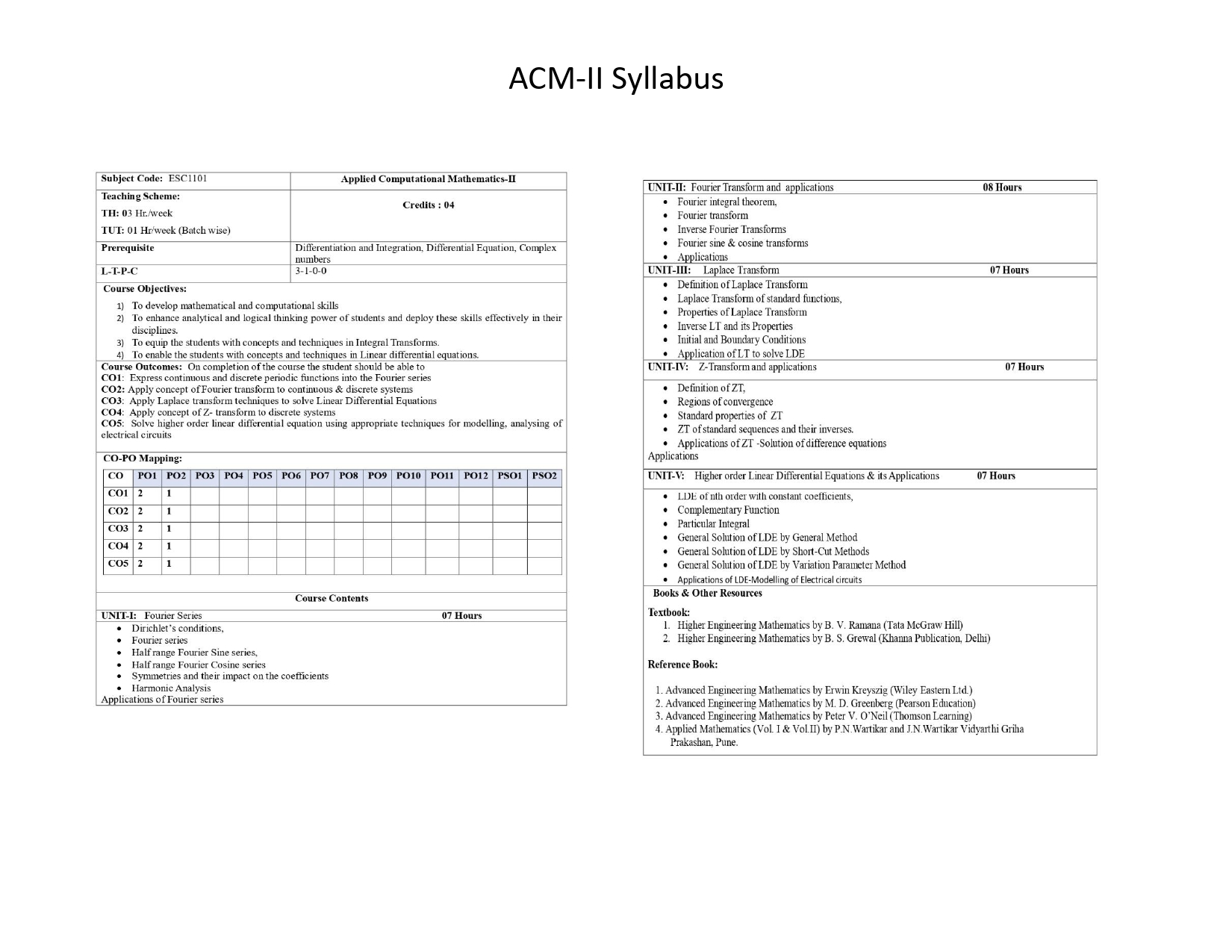
Subject Code:  ESC1101

Applied Computational Mathematics-II

Teaching Scheme:

TH: 03 Hr./week

TUT: 01 Hr/week (Batch wise)

Credits : 04

Prerequisite

Differentiation and Integration, Differential Equation, Complex numbers 

L-T-P-C

3-1-0-0

Course Objectives:

1)      To develop mathematical and computational skills

2)      To enhance analytical and logical thinking power of students and deploy these skills effectively in their disciplines.

3)      To equip the students with concepts and techniques in Integral Transforms.

4)      To enable the students with concepts and techniques in Linear differential equations.

Course Outcomes:  On completion of the course the student should be able to

CO1:  Express continuous and discrete periodic functions into the Fourier series

CO2: Apply concept of Fourier transform to continuous & discrete systems

CO3:  Apply Laplace transform techniques to solve Linear Differential Equations   

CO4:  Apply concept of Z- transform to discrete systems  

CO5:  Solve higher order linear differential equation using appropriate techniques for modelling, analysing of electrical circuits

CO-PO Mapping:

Course Contents

UNIT-I:   Fourier Series                                                                                             07 Hours

·         Dirichlet’s conditions,

·         Fourier series

·         Half range Fourier Sine series,

·         Half range Fourier Cosine series

·         Symmetries and their impact on the coefficients

·         Harmonic Analysis

Applications of Fourier series

UNIT-II:  Fourier Transform and  applications                                                            08 Hours                                                                                                                                       

·         Fourier integral theorem,

·         Fourier transform

·         Inverse Fourier Transforms

·         Fourier sine & cosine transforms

·         Applications

UNIT-III:     Laplace Transform                                                                                     07 Hours

·         Definition of Laplace Transform

·         Laplace Transform of standard functions,

·         Properties of Laplace Transform

·         Inverse LT and its Properties

·         Initial and Boundary Conditions

·         Application of LT to solve LDE

UNIT-IV:    Z-Transform and applications                                                                            07 Hours                                                                                                                                                            

·         Definition of ZT,

·         Regions of convergence

·         Standard properties of  ZT

·         ZT of standard sequences and their inverses.

·         Applications of ZT -Solution of difference equations

Applications

UNIT-V:    Higher order Linear Differential Equations & its Applications               07 Hours

·         LDE of nth order with constant coefficients,

·         Complementary Function

·         Particular Integral 

·         General Solution of LDE by General Method

·         General Solution of LDE by Short-Cut Methods

·         General Solution of LDE by Variation Parameter Method

·         Applications of LDE-Modelling of Electrical circuits

Books & Other Resources

Textbook:

1.      Higher Engineering Mathematics by B. V. Ramana (Tata McGraw Hill)                                

2.      Higher Engineering Mathematics by B. S. Grewal (Khanna Publication, Delhi)

Reference Book:

   1. Advanced Engineering Mathematics by Erwin Kreyszig (Wiley Eastern Ltd.)

   2. Advanced Engineering Mathematics by M. D. Greenberg (Pearson Education)

   3. Advanced Engineering Mathematics by Peter V. O’Neil (Thomson Learning)

   4. Applied Mathematics (Vol. I & Vol.II) by P.N.Wartikar and J.N.Wartikar Vidyarthi Griha 

       Prakashan, Pune.

Theory & Tutorial/Practical Class

Tutorial:

i) Tutorial for the subject shall be engaged in minimum three batches (batch size of 22 students maximum) per division.

ii)  Term work shall consist of five assignments on each Unit-I to Unit-V and is based on performance and continuous internal assessment.